近日，我院微纳电子材料与新型信息器件课题组曾波文博士在关于非厄米拓扑边缘态的拓扑表征取得重要进展。研究结果显示边缘态可看成本征方程的特殊解，从而在非厄米SSH模型中得到非厄米边缘态的一般解，并逆向构建拓扑元组分别表征边缘态的存在性和空间分布，为边缘态的调控和应用、拓扑局域和非厄米局域的竞争提供了全面的理解。论文以《Inverse design of winding tuple for non-Hermitian topological edge modes》为题，以Letters形式发表于凝聚态物理顶级期刊《Physical Review B》。曾波文博士和华中科技大学胡勇教授为该论文的共同通讯作者，304am永利集团物理与电子科学学院为共同通讯单位。

   

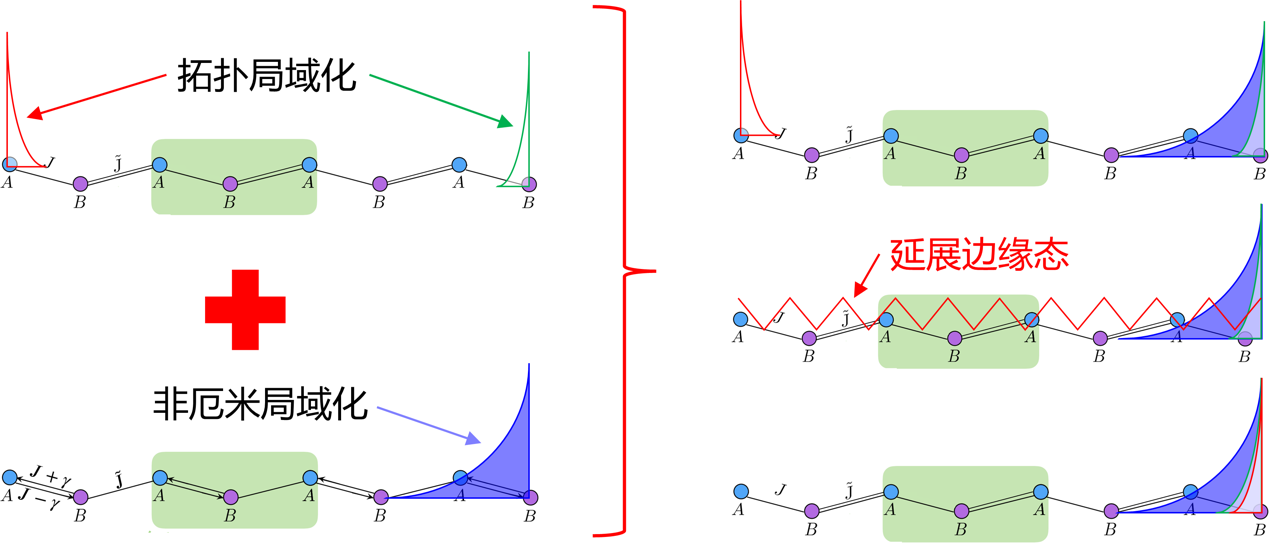
图1 拓扑局域和非厄米局域化的竞争。

拓扑局域化与非厄米局域化在非厄米晶体系统中的相互作用，导致拓扑边缘态呈现出多样化的形态分布，这为调控边缘态以实现潜在拓扑应用提供了契机。传统拓扑不变量计算无法提供边缘态波函数的详细信息，而精确表征边缘态作用域并实现其调控恰恰需要这些信息。论文通过将边缘态看做为特征方程的特定解，推导出扩展型非厄米SSH模型中边缘态的波函数，进而逆向构建了可同时表征边缘态存在性及其空间分布的绕数元组。此外，论文定义了等效的谱绕数，该量由不同能带能量的乘积决定。这种拓扑不变量的逆向设计方法，使得即使在缺乏子晶格对称性的系统中也能对边缘态的局域特性进行分类，这将显著促进不同量子材料与器件研发中边缘态的调控与利用。

                                  

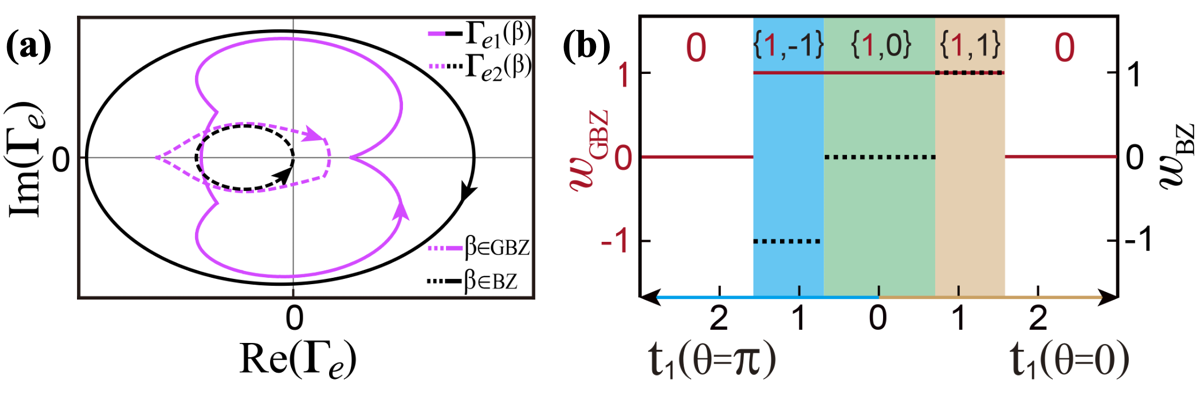
图2 (a)波矢随GBZ和BZ演化，(b)表征拓扑边缘态的拓扑元组。

该项工作得到了湖南省自然科学基金和Innovation Program for Quantum Science and Technology项目的支持。

文章链接：https://journals.aps.org/prb/pdf/10.1103/PhysRevB.111.L041406